Operational Amplifier (運算放大器)

Operational Amplifier
Operational Amplifier (OP Amplifier)
運算放大器
Operational Amplifier (運算放大器)
運算放大器 (Operational Amplifier; OP Amplifier)

Source:

http://mysite.du.edu/~etuttle/electron/elect3.htm

Operational Amplifiers--DC

---

Op-Amp Fundamentals

Operational amplifiers, or op-amps for short, got their name from the modules used in analog computers to perform "operations" such as adding, multiplying and so forth. Now they are integrated circuits for application as general feedback amplifiers. They seem easy to use, but the many types available and the great variety of ratings hint that their use requires considerable knowledge and skill, which is very true. In this page, I will present a dozen or so circuits that will give a good understanding of how to use op-amps in DC applications, where an oscilloscope is not needed. Most of the really interesting uses of op-amps involve changing signals, but this topic will be reserved for later.

The power supply for an op-amp is normally bipolar, with voltages above and below ground, called +V and -V. Most common op-amps can stand up to 36V, or ±18V. It is convenient for our experiments to use ±12V, which is usually available from multi-ouput power supplies. You can always arrange a bipolar supply from two ordinary supplies. Ground in this case is merely a voltage between the supply rails, as they are called, of no special significance. Op-amps have no ground terminal, since this reference is unnecessary. If you have trouble remembering polarity, have lots of op-amps around, since they are instantly destroyed by any mistake.

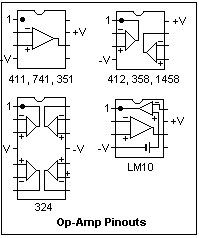The pinouts of several common op-amps are shown in the figure. These are the usual DIP packages, as seen from the top, with pins numbered from upper left, down one side and up the other to upper right. The 411 is a JFET-input op-amp quite suitable for our purposes. The 741 is a bipolar op-amp, long a standard. These two op-amps can be used interchangeably in most circuits. The dual 411 is the 412, and the dual 741 is the 1458. The 351 is another popular JFET-input op-amp. The 324 comes four to a package, and two to a package in the 358. The LM10 includes a voltage reference and an op-amp to buffer it, in addition to the main op-amp. The cheapest LM10 is the LM10CL version, which has a 7V limitation on the power supply. It is useful when only +5 is available. Don't use it with the usual ±12V supply!

The connections marked + and - are the inputs to the op-amp, and the connection from the point of the triangle is the output. The output can go from a value near +V to a value near -V. When the ouput is near one of these limits and can go no farther, it is said to besaturated. You can short-circuit an output if you want, since it is internally protected against too much current. On the other hand, the output will handle only up to about 20mA at best. Op-amps are not for power applications, but can drive a power amplifier (usually transistors) if power is needed. The output is proportional to the difference in voltage v₊ - v_- between the two inputs, where v₊ is the voltage at the + or noninverting input, and v_- the voltage at the - or inverting input. The voltage gain of the amplifier is perhaps 100,000 or 100 dB at low frequencies. With such a gain, the voltage between the inputs must be very small if the output voltage is not to be at saturation. This amounts to a rule: the voltages at the inputs are equal when a circuit is working properly.

In order to make the voltages at the inputs equal to each other, it is necessary to arrange this by feedback. All op-amp circuits use feedback, and the properties of the circuit are determined by the feedback, not by the properties of the op-amp. It's best to study op-amp circuits with no reliance on feedback theory, and to use the results to understand and appreciate feedback theory instead. Then one can come back with greater knowledge to handle more difficult cases.

The common-mode input signal is the average of the potentials of the two input connections. Since they are usually at the same voltage, this voltage is the common-mode input voltage. The op-amp ignores the common-mode input, and determines its output only by the difference signal. Nevertheless, it is important to look at the common-mode input voltage and see that it does not leave its permissible range. The common-mode range of an op-amp is less than from +V to -V, and the op-amp usually does something unpleasant when the range is exceeded (the 411, for example, goes from a large negative output suddenly to a large positive output when this happens). Some early op-amps had a very limited common-mode range. In the LM10 and the 324, the common-mode range goes to -V (as does the output voltage), which makes these op-amps suitable for a +V to 0 supply.

That the inputs are usually at the same voltage does not mean that they can be connected to each other. If you do this, the output usually saturates. The voltages must be held equal by the active participation of the output, acting through the feedback network. The inputs also carry a small dc bias or leakage current that must have a route to the power supply. With bipolar op-amps, this current is actually the base bias current for the input transistors, and sometimes has to be considered in the circuit design. JFET's, on the other hand, have a much smaller input current that is largely leakage, and does not affect the circuit much--except that it has to have a route to ground. In ordinary circuit analysis, the bias currents can be neglected, and it can be assumed that the inputs carry no current. Don't forget that this is only approximate!

The most important factor hidden from the casual user of op-amps is the question of stability. Stability is always important with high-gain amplifiers, and when feedback is applied. The feedback loop can become the route for a signal to be fed back to the input in the proper phase to cause oscillation, called instability. Without some care, feedback always results in instability, which is always fatal. The oscillation can occur either at a higher or a lower frequency than that for which the circuit is designed, usually higher (like the feedback with a microphone and speaker). With the ordinary op-amps, stability is guaranteed by making the gain fall off at 20 dB per decade of frequency, beginning at about 10 Hz, so that the gain of the amplifier falls to unity at around 1 MHz. Unless you have capacitors in unfortunate places, this guarantees that the circuits you put together will be stable, no matter what you do. What you pay for this is a severe restriction on the bandwidth of op-amp circuits, and overcoming it is advanced work.

It may be useful to restate here the assumptions that make the analysis of op-amp circuits easy. First, the inputs carry no current. Second, proper feedback acts to make the voltages at the inputs equal. To check that the feedback is proper, suppose the noninverting (+) input to rise slightly in potential. This makes the output voltage increase; if this increase acts to raise the potential of the inverting (-) input, then the feedback is correct (negative). Finally, there must always be a conductive path from either input to ground.

Circuits

You will need, in addition to the bipolar power supply, three op-amps (more if you cannot keep power polarity straight), two 10k pots, and resistors of 100, 1k, 10k and 100k values. A couple of the circuits involve transistors, and a 100Ω, 1W resistor is needed as a load in one circuit. Most of the circuits are simple, but a few can be a challenge. There are two ways to construct a fairly complex circuit on the breadboard. One way, the one I use, is to wire things in logically, looking up the proper pins at the time. The other way is to sit down with the pinouts and the circuit diagram and label each connection with its pin number, then make the connections accordingly, not worrying about what you are connecting. The first method is faster and more intuitive, while the second can avoid mistakes, especially when you are dealing with integrated circuits with lots of pins. In either case, the circuit diagram is the basic reference.

The first example is a precision voltage divider. The voltage output of a divider depends on its load, and if the slider of the potentiometer happens to be grounded, the pot will be destroyed should the slider inadvertently (and inevitably) be moved to the wrong end. This circuit overcomes both these problems, and you may want to use it as a voltage source for the later examples. The inverting input is tied to the output, and the noninverting input is tied to the pot slider. The output will be driven to a voltage equal to that of the slider as it strives to keep the inputs at the same voltage. If it goes a little too high, the - input will drive it lower; if it goes too low, the opposite will happen. The feedback is negative and stable. No current is drawn by the pot slider (the tiny bias currents leave through the potentiometer resistance causing negligible voltage drops). The common-mode input is equal to the pot setting. If you try to drive it too, far, the op-amp will go wild. With a ±12V supply, the circuit is good for ±10V in any case.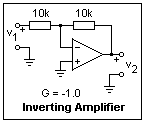

This is the familiar inverting amplifier circuit. The output must strive to keep the - input at ground whatever voltage you apply at the input. The circuit is easily analyzed to give a gain equal to the negative of the ratio of the feedback resistors. In this case, G = -1. Try a few values of the input, positive and negative, and measure the output voltage. As usual, two meters make this work much more pleasant. The - input is at ground (which can be verified with your meter), but connecting it with ground would destroy the functioning. This is called a virtual ground. If you connect more inputs to it, each with its resistor, you will get a summing circuit. What is the common-mode input voltage in this circuit?

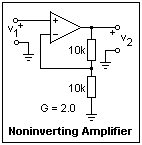The feedback is again from the output to the - input, through a voltage divider. The output strives to hold the - input equal in voltage to the + input, but here the voltage of the + input is the input to the circuit. This is exactly the same circuit that we considered in the preceding paragraph, except that the input is now at the terminal that was grounded there, and the old input is now grounded. This circuit is as easily analyzed, with the result that the gain is positive, and is 1 plus the ratio of the resistors. So, here we expect a gain of G = +2. Make some measurements to verify this. What is the common-mode voltage here?

The input resistance of a circuit is the ratio of an applied voltage to the current that results. In the inverting amplifier, it is equal to the input resistor, while in the noninverting amplifier, it is very large. However, bias currents must still have a way out (they do not affect the input resistance) even if they are not appreciable. The output resistance of an amplifier is the ratio of the voltage drop when the amplifier is loaded, to the current drawn from it. Attach a load of 1k to 10k to the amplifiers above, and see how much the output voltage drops. The output resistances are very small in either case. The drawback of the inverting amplifier is the low input resistance, while the drawback of the noninverting amplifier is the common-mode input.

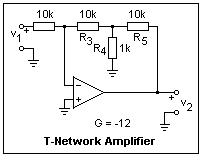To get a large voltage gain, a large feedback resistor is needed. These large resistors can be troublesome, and it is possible to use much smaller resistors in the T-network shown in the figure. Here we have used rather small resistors so that the gain will not become inconveniently large for us to measure, but the equivalent resistance R₃(1 + R₅/R₄) = 110k, though the largest resistor used is 10k. The idea is simply to make the output less effective at the - input. Check that the gain of this amplifier is G = -12. Using this trick allows us to use a larger input resistor, making the input resistance larger.

A voltage standard, whose potential does not vary with load or temperature, is easily achieved with an op-amp. In this case, a noninverting amplifier with a gain of +2 is used, but a simple unity gain buffer is also possible. The voltage reference is an LM336, shown as a Zener diode. By means of the adjustment terminal, the voltage can be trimmed to any desired close-by value. 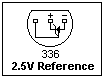The exact value is usually not as important as the stability of whatever value occurs. The pinout of the LM336, which is furnished in a TO-92 package, is shown at the left. By means of the 10k pot, the output voltage of the circuit was varied from 4.69 to 5.25V. The LM10 has an internal voltage reference of 200 mV, which is very convenient. Zener diodes can also be used as voltage references, but the integrated circuits designed for this purpose are much more stable and accurate.

A potentiometer is used in the feedback loop to give a variable gain to the amplifier. The gain does not vary linearly with potentiometer position, since it is equal to 1/K, where K is the fraction of the pot resistance to the left of the slider. Hence, the gain varies from 1 to infinity. It would possibly be a good idea to add a fixed resistance to the left of the pot to limit the gain to some large value. Measure the gain for some position of the slider, and then used your meter to find KR, and hence K, and compare the measured gain with 1/K.

This circuit is another kind of gain control, where the gain can vary from -1 to +1. The input impedance is rather low, but the control could be preceded by a buffer. Also, an amplifier of fixed gain could follow, so that the gain could be varied from -G to +G.

Sometimes we want a voltage to current converter, that will turn a voltage into a proportional current. Of course, a simple resistor can do this, but then the current will depend on the load resistance. Ideally, a current source should have an infinite output resistance (so that any load resistance would be a negligible fraction, keeping the current constant), and a simple resistor does not satisfy this requirement very well. The circuit shown here has a nearly infinite output resistance, since the output current is equal to the current through resistor R, which is v₁/R. The output of the op-amp changes its voltage so that this current flows, whatever the load resistance. Use your meter on a current scale for the load. Connect a resistance (say, 1k) in series with the meter to see that you get the same current.

The previous circuit had the disadvantage that neither terminal of the load was at ground. Such a load is said to float, and must be allowed to vary as the circuit requires. The circuit shown at the right has a load with one terminal grounded, which is usually much more convenient. This circuit is called a Howland current source. It is not really a very good current source; even trimming the resistors does not improve it very much. I found a Norton resistance of about 5kΩ. However, it is an interesting circuit. The analysis of this circuit can start by assuming some unknown voltage v at nodes a and b. The feedback will act to keep these nodes at the same potential, in the usual fashion. Now the currents in the branches to the left of these nodes can be written down, and the voltage at the third node, c, can be determined. Now all currents flowing into node b can be found, and the load current is found to be the input voltage divided by the resistance in the other input, 1k in this case, provided the ratios of the resistances are equal as shown. Test this circuit to see that is produces the advertised current in response to the input voltage.

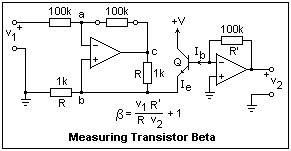The circuit shown in the figure at the left is for determining the beta of transistors, consisting of a voltage-to-current converter on the left, and a current-to-voltage converter on the right. A resistor is also a current to voltage converter, but we would like a zero input resistance so that the voltage at the input will not change if we vary the current. The circuit shown to the right of the transistor in this figure is a current-to-voltage converter, simply an inverting amplifier with no input resistor. The current flows into a virtual ground, whose potential is not affected by the current, while the output voltage is proportional to the input current.

The circuit to the left of the transistor is a voltage-to-current converter that supplies emitter current to the transistor, while base current is supplied by the current-to-voltage converter on the right. The base of the transistor is held at ground, so the output of the emitter current source must be at -V_be. The emitter current is set by the voltage input to the V-to-I converter, and the resulting base current measured by the voltage output by the I-to-V converter. The beta of the transistor is one plus the ratio of the emitter to the base current (the emitter current is the collector current plus the base current, of course). It is really simple and quick to measure the beta of transistors with this circuit, and you might try it on several examples. The dependence of beta on collector current is easy to observe with this circuit.

The output of an op-amp will source or sink only about 20 mA, not enough really to provide any kind of power. However, transistors can be used to help, and to provide as much current as is necessary. The circuit shown uses an npn and a complementary pnp transistor to supply current for both polarities. Only one of the transistors is conducting at a time. If the supply is unipolar, only one transistor is necessary. It is good to be careful that the base-emitter junction is not broken down by too large a reverse voltage (greater than about 5V). In this case, the op-amp could at most create a voltage drop of 2V in the 100Ω resistor, so the emitter junctions are safe in this circuit. Actually, even if the resistor were not there, the reverse voltage would not exceed the base to emitter drop of the other transistor.

The important thing to note in this circuit is that the feedback loop is closed around the whole circuit, so that the output voltage is accurate. The outputs must supply an additional voltage to turn the transistors on. When the output is 10V, the op-amp is supplying 10.7V (close to saturation). The load in this circuit is a 100Ω resistor. With 10V across it, the current will be 100 mA, and it will dissipate 1W. Therefore, use at least a 1W resistor for the load, not the usual 1/4W resistors, which will certainly get too hot. Test the circuit, observing that you can get more than 20 mA output, and that the output can swing both positive and negative.

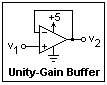Take a 324 op-amp and connect +5 and ground as power. The connections are rather unexpected, so take care. The +5 seems to me to be on the wrong side! Note how the power supply is represented in a circuit diagram when necessary. Usually, the power supply is not shown explicitly. Construct a unity-gain buffer as shown, and feed it with a potentiometer also connected between +5 and ground. Find the range of the output voltage (or common mode range). I found 0 to 3.89V. The range 0 to V - 1.5V is guaranteed in the specifications. It is quite remarkable that the op-amp will operate on such a small voltage, and that both the common mode and the output voltage range go to zero.

Here is another test circuit, while you have a 324 connected to +5. It is a voltage to current converter driving an LED. Measure the voltages at nodes a, b and c and consider them. I did not get the voltages at nodes a and b quite equal; this is probably a result of an input voltage offset, or bias currents. The 324 has a bias current of about 1 μA, which I determined by experiment on a sample.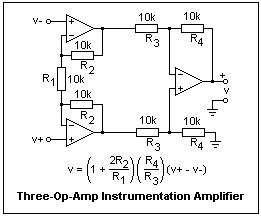

This is an important circuit, the so-called three-op-amp "instrumentation" amplifier. Before building it, change back to a bipolar ±12V supply for convenience. It requires seven resistors, here all 10k, which gives a gain of 3. The gain is changed by changing R₁. For example, if R₁ = 1k, the gain becomes 21. It is best to leave R₃ = R₄ in any case, since this gives the best common-mode rejection. It is a differential amplifier, with inverting and noninverting inputs of very high impedance, so they will not load the circuit to which they are connected. The output should not change if both inputs are connected to the same voltage and this voltage varies--this is what is meant by common-mode rejection. If you use 1% resistors, this circuit gives very good results, and is quite practical. 1% resistors are not only precise in value, but are much more stable than the usual 5% resistors. It is best not to make R₁ a potentiometer, since potentiometers are much less reliable than simple resistors. There should be no need to trim the gain to some exact value. Of course, this can be done if desired. With the 324, there are enough op-amps in a single 14-pin DIP, with one left over for other duties.

References

1. J. R. Hufault, Op Amp Network Design (New York: John Wiley and Sons, 1986). An extensive collection of practical op-amp circuits, with many excellent hints and ideas. On p. 136, the polarity of the inputs of the upper op-amp is reversed.

---

Return to Electronics Index

Composed by J. B. Calvert
Created 4 July 2001
Last revised 19 September 2008